Intoduction

Chapter 1 in the Sage Handbook of Social Network Analysis

PREPRINT VERSION

Citation
John Scott, John McLevey, and Peter Carrington. 2023. “Introduction” in John McLevey, John Scott, and Peter Carrington (eds) The SAGE Handbook of Social Network Analysis (Volume 2). London, UK: SAGE.

This new edition of the Sage Handbook of Social Network Analysis aims to build on the success of its predecessor, bringing together in one place a comprehensive overview of social network analysis produced by leading international scholars in the field. We present authoritative accounts of its history, theories, and methods, and a wide-ranging review of the various disciplines and topics to which it has made important contributions. Most of the topics covered in the first edition are included here, but in thoroughly revised or new chapters, many by new authors. We have also included chapters on a number of new topics that have experienced significant development since the first edition appeared, in order to ensure that the volume is completely up to date and so continues to meet the needs and expectations of our readers. In what follows, we provide a high-level overview of the development and growth of social network analysis and discuss several ideas that are foundational to the field.

The Development of Social Network Analysis

The idea of social structure has been central to sociological thought from its earliest days, but it was not until the early twentieth century that the idea of the social network began to be used as a metaphor in sociological analysis to represent the features of social structures.¹

This was, perhaps, especially marked in German sociology, where there was a concern to understand the complex interweaving of social relations into ‘figurations’ and ‘webs’ of connections. Georg Simmel argued that ‘society merely is the name for a number of individuals connected by interaction’ (1950 [1917]: 10), and that the task of sociology is to investigate the forms, or structure, of those interactions through ‘geometrical abstraction’ (Ibid., pp. 21-22). He and his followers developed a ‘social geometry’ that emphasised the formal properties of these patterns of connection and introduced a novel terminology that referred to ‘points’ and ‘lines’ to understand actors and their social relations.

These formal ideas were first systematized by Helen Bott (1928), Jacob Moreno (1934), and Kurt Lewin (1936) in their studies in social psychology and psychotherapy. They were concerned with how the structures of small groups influenced the perceptions and action choices of their individual members. To this end, they treated a group as a ‘field’ or ‘space’ of activity that could be explored mathematically. Moreno and Helen Jennings referred to this approach as ‘sociometry’, or ‘psychological geography’ – the measurement and mapping of social relations – and invented the ‘sociogram’ as a way of visually representing social networks as patterns of points and lines. Sociometric investigations were undertaken in education (Jennings, 1948; Gronlund, 1959) and community studies (Lundberg and Lawsing, 1937; Lundberg and Steele, 1938). Later work in social psychology developed this as ‘group dynamics’ (Cartwright and Zander, 1953; Harary and Norman, 1953), an approach that was furthered at the University of Michigan and at the Tavistock Institute in London.

George Lundberg’s insights into community relations had a wider impact through the work of Lloyd Warner in the studies, undertaken with Elton Mayo, of the Hawthorne electrical works in Chicago (Roethlisberger and Dickson, 1939). The Hawthorne researchers were inspired by the sociometric studies in seeking visual representations of social relations, but they were also directly influenced by the electrical wiring diagrams used in the Hawthorne factory and saw wiring networks as a model for representing group relations. Warner built on this early research in investigations into the community structures of American towns and cities. Influenced by the work of the British anthropologist Alfred Radcliffe-Brown, Warner looked at the structure of group relations in large communities and used network diagrams to represent their social structures. In his study of the New England town of Newburyport, carried out between 1930 and 1935, Warner presented large-scale community relations in matrix form, showing that group relations could be represented in mathematical terms and that these mathematical structures could be transformed into a visual representation. Central to Warner’s concerns was an exploration of the formation of ‘cliques’ within large urban social networks (Warner and Lunt, 1941). In a justly famous commentary, George Homans (1950) used these matrix methods to reanalyse a small clique of women studied by Warner in the southern town of Natchez.

A crucial advance in social network analysis took place at the University of Manchester in the 1950s. A group of sociologists and social anthropologists working on African and European communities and critical of the mainstream emphasis in American sociology on consensus and harmony, sought to place conflict and division at the centre of their analyses. They were strongly influenced by the ‘structuralist’ view of society that had been expounded by Radcliffe-Brown since the 1920s, his public lectures delivered in 1937 and 1940 referring explicitly to the ‘network of social relations’ and its ‘social morphology’ (Radcliffe-Brown, 1940; 1957). Working closely with the Manchester scholars, John Barnes and Elizabeth Bott allied this approach with the group dynamics being developed at the Tavistock Institute and with the work of Warner. In a Norwegian study, Barnes (1954) proposed that the metaphor of the network of relations be taken seriously as a way of exploring the warp and weft of community relations, and in a study of kinship in London, Bott (1955; 1956) employed ideas of connectedness and density in urban kinship relations. Under the influence of a systematic study by Siegfried Nadel (1957), the developing Manchester work on African communities was reported by Clyde Mitchell (1969b), who also provided one of the earliest summaries of a formal social network methodology (1969a). The role of kinship in social cohesion considerably extended and elaborated since those early works (White, 2011).

Simultaneously with the work of Mitchell and his associates was the work of a group of American researchers led by Harrison White, who had also begun to develop and apply formal, mathematical methods for social network analysis. Building on the work of Claude Lévi-Strauss (1969 [1949]) in collaboration with André Weil, White (1963a) used algebra to represent kinship structures. When White moved from Chicago to Harvard University, he formed a large and dynamic group of students and associates to develop a paradigm for network analysis (see Mullins, 1973: chap. 10). These researchers included Joel Levine’s (1972) work on corporate power as a multidimensional field, Nancy Lee’s (1969) research on the role of communication networks in helping American women find doctors willing to perform an abortion prior to Roe v. Wade, Mark Granovetter’s (1973; 1974) comparison of the role of ‘strong’ and ‘weak’ ties in searches for employment opportunities, and Nick Mullins’ (1973) network analysis of mid-20th century American sociology. White himself worked with various colleagues on algebraic methods for representing and analysing systems of social positions and roles (Lorrain and White, 1971; Boorman and White, 1976; White et al. 1976). This group constituted a new generation of social network researchers who helped to spread social network analysis across the globe. White went on to formalise his approach in a classic, but complex text (2008; see also Azarian 2005).

One of the principal areas in which social network analysis has been applied is the investigation of corporate power and interlocking directorships (Carroll et al., this volume). Early studies by Paul Sweezy (1939) and others had adopted ad hoc techniques for drawing network diagrams of board-level connections, but it was not until the 1960s and 1970s that these suggestions were furthered as a result of the technical advances made by White and his associates. Joel Levine (1972) documented the clusters formed by particular banks and their directors, and a path-breaking paper by Jim Bearden and his colleagues (2002 [1975]) used the idea of centrality to explore the power and influence of banks in the American corporate world. Elsewhere, work led by Rob Mokken and Frans Stokman in the Netherlands (Helmers et al., 1975) became the basis for an investigation of transnational patterns (Fennema, 1982) and an international comparative investigation (Stokman et al., 1985; and see Scott and Griff, 1984). This was extended into a comparative investigation of intercorporate shareholding networks (Scott, 1986) and led to numerous studies in a variety of societies (see the reviews in Scott, 1997 and the comparative study edited by David and Westerhuis, 2014).

Another important area of application has been the investigation of community structure. Rooted in Warner’s studies, it was again a number of researchers influenced by the developments at Harvard who pushed this area forward. Claude Fischer (1977) and Barry Wellman (1979) undertook work that completely reoriented the research area. Wellman carried out a series of investigations into the changing structure of friendship in the social integration of communal relations in a Canadian city. His particular concern was to investigate the changing ways in which people maintained contact with each other, and his thesis was that each individual has his or her own personal ‘community’, consisting of those to whom they are socially connected (Chua et al., 2011). Reconceptualising community as formed of personal networks, or egonets (Perry et al., this volume), liberated community study from its previous spatial bounds in the neighbourhood. Wellman was also an important early contributor to research on the impact of electronic communication on the structure and operation of interpersonal networks (Wellman and Hogan, 2006). This work led to the development of a now-thriving literature on social media and online communities (Quan-Haase, this volume), as well as networks of social support (Song and Zhang, this volume). It also influenced studies of ‘social capital’ (Völker, this volume), which developed from the varying works of Robert Putnam (2000) and Pierre Bourdieu (Bourdieu and Passeron, 1970). Nan Lin (2001) and Ronald Burt (2005; see also Lin et al. 2001) also made influential contributions to this literature.

The structuralist orientation of social network analysis put it at odds with concepts such as culture, identity, and agency for much of the field’s early history, but this started to change in the early 1990s. For example, White (2008 [1992]), Emirbayer (Emirbayer and Goodwin, 1994; Emirbayer, 1997; Emirbayer and Mische, 1998), and Mische (2003) began to theorize the foundations of a ‘relational sociology’ (Mische and Fuhse, this volume), building on White’s approach to culture and identity. Other approaches to relational sociology (Donati, 2012) that utilise social network analysis have also developed, most markedly in the work of Nick Crossley (2010; 2021).

Beyond “relational sociology,” research at the intersection of networks, culture, language, cognition, and affect has been thriving in recent years (Lizardo, this volume; Shugars and González-Bailón, this volume; Brashears and Money, this volume; Agneessens, this volume). This work, together with advances in modelling scientific (Kang and Evans, this volume) and socio-ecological networks (Bodin, this volume), has contributed to the development of methods and models for multi-modal (Jasny, this volume) and multi-level networks (Lazega and Wang, this volume).

Numerous other applications have extended social network analysis beyond sociology and anthropology into other disciplines, such as history (Kumekawa, this volume), geography (Hipp, this volume), environmental science and policy (Bodin, this volume; Scott et al., this volume) and economics (Goyal, 2011). Network analysis has also been used to make important contributions to interdisciplinary research on subjects such as political and policy networks (Diani, this volume; Knoke, 1990; Knoke et al., 1996; Knoke, 2011), social movements (Tindall, this volume; Diani, 1995, 2011), gender and ethnicity (Bellotti, this volume; Côté, this volume), crime (Ouellet, this volume; Morselli, 2009; Arquilla and Ronfeldt, 2001), terrorism (van der Hulst, 2011), international trade (Prell et al., this volume) and the world political economy (Kick and Davis, 2001; Kick et al., 2011; Carroll et al., this volume), diffusion (Centola, this volume), the impact of peers on attitudes and behaviour (Kirke, 2006; An, 2011), health outcomes (de la Haye, this volume); and many other topics.

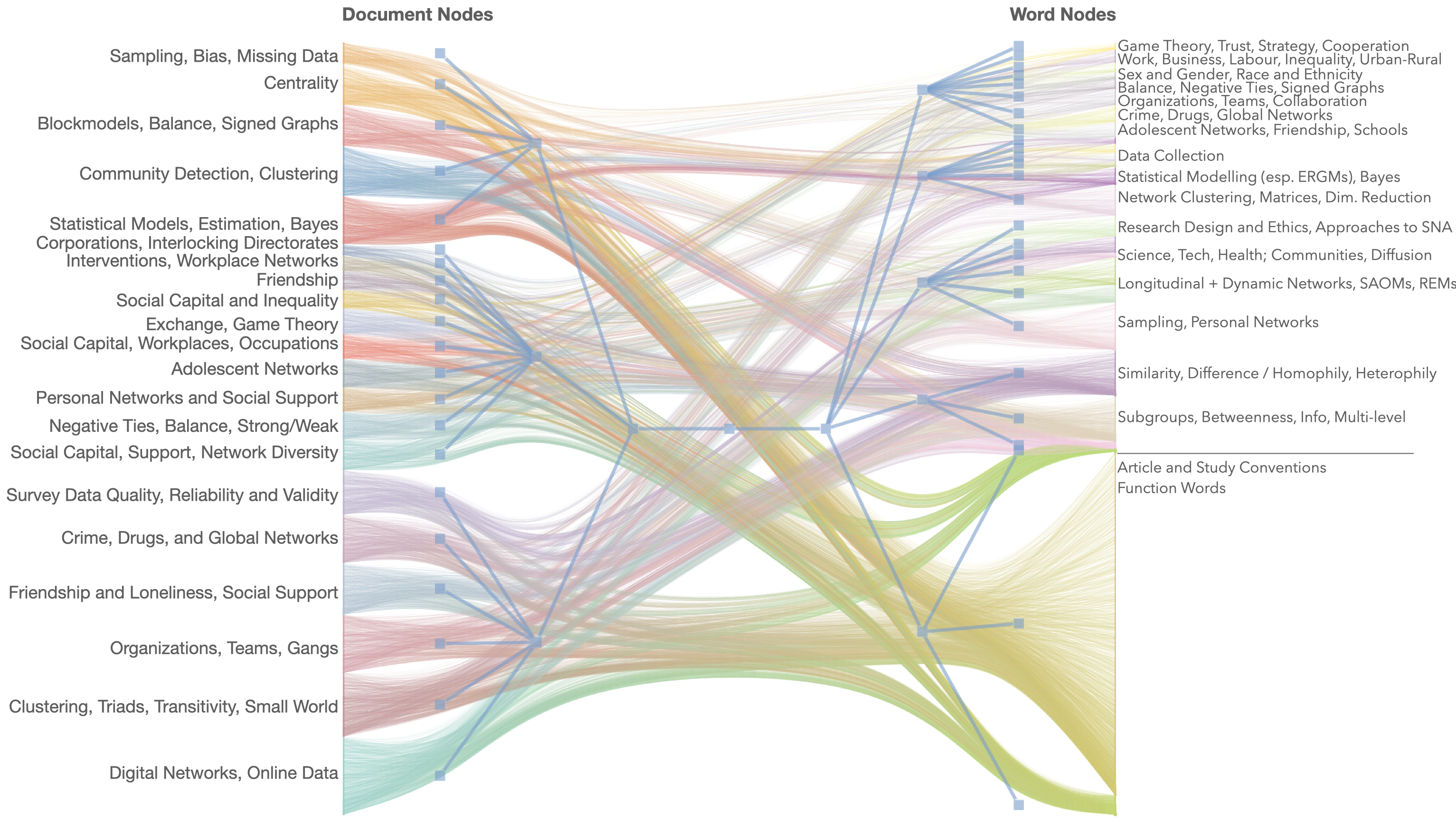
Since the late 1970s, there has been a huge increase in technical contributions to social network methodology and in its application (e.g., Burt 1982; Holland et al. 1983; Freeman et al. 1989; Wasserman and Faust 1994; Wasserman and Galaskiewicz 1994; Hoff et al. 2002; Brandes and Erlebach 2005; Carrington et al. 2005; Butts 2008; Snijders et al. 2010; Lusher et al. 2013). The importance technical contributions in SNA is evident when we take a high-level view of the field. For example, we analysed the latent topic structure of all publications in Social Networks by fitting a hierarchical Bayesian stochastic blockmodel to a bipartite network of journal articles and the words contained in their titles and abstracts (see Gerlach et al. 2018 for a discussion of network-based generative topic models, and Browne, Crick, and McLevey, this volume, for Bayesian stochastic blockmodels). Our analysis detected 26 latent topics (at the lowest level of the model), 20 of which are substantively interesting.²

Figure 1 is a visualization of the hierarchical blockmodel, with word nodes clustered into latent topics on the right, and document nodes clustered based on their topic mixtures on the left. The hierarchical blockmodel is superimposed, with square blue nodes, over the original complex network. We focus on the lowest levels of the blockmodel, which are the blocks furthest to the right (topics) and left (document clusters) of the graph.

Figure 1: Visualization of a hierarchical Bayesian stochastic blockmodel fit to the bipartite network of Social Networks articles and the words contained in their titles and abstracts. The nodes on the right are words, clustered into mixtures of latent topics. The nodes on the left are documents, clustered based on their latent topic mixtures.

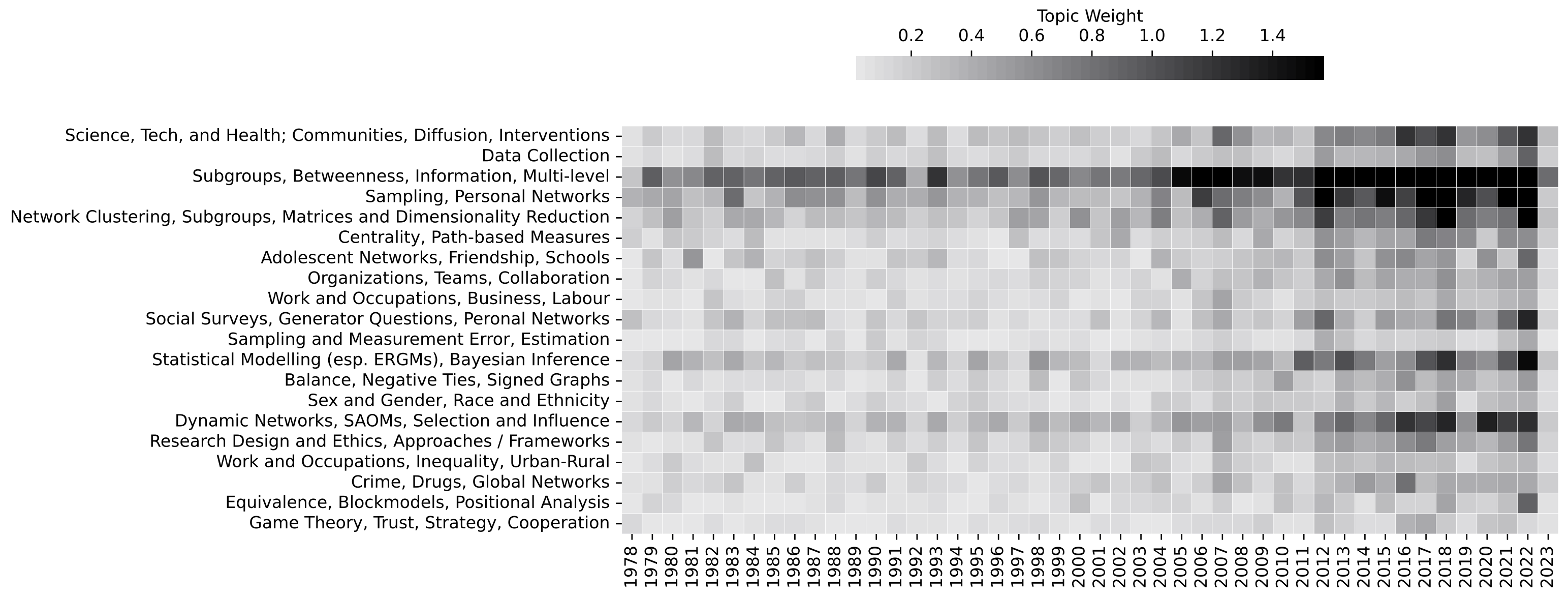
To interpret each latent topic, we read the full list of associated words, as well as the titles and abstracts of articles that prominently feature the topic, and the titles and abstract of documents belonging to document clusters that prominently feature the topic. We then assigned each a general label, computed the distribution of topics over all Social Networks publications, and aggregated the results for each year to examine change over time. Those results are shown in Figure 2, which compares the weight of each detected topic over time.

Figure 2: Changes in the topics covered by Social Networks publications over time.

Our model results illustrate the importance of technical contributions to social network analysis since Social Networks was founded in the late 1970s. For example, we see technical work on network clustering, partitioning, and dimensionality reduction (Moody and Mucha, this volume, Dorien et al., this volume; Browne, Crick, and McLevey, this volume); relational data collection, sampling, and measurement (adams and Lubbers, this volume); statistical modelling, in particular exponential random graph models (Koskinen, this volume), stochastic actor-oriented models (Snijders and Steglich, this volume), and relational even models (Schecter and Contractor, this volume); as well as centrality and related measures (Everett and Borgatti, this volume). We also see topics representing developments in methods and models for negative ties and signed graphs (Agneessens, this volume), as well as multi-modal (Jasny, this volume) and multi-level networks (Lazega and Wang, this volume); and models of diffusion, opinion dynamics, and network interventions (Centola, this volume; Valente, this volume).

Some of these developments, at various points in SNA’s history, are the result of interdisciplinary engagement between sociology and other social sciences on the one hand, and physics and other natural sciences on the other. While social network analysis has long had meaningful connections to physics (e.g., Harrison White earned two PhDs, one in theoretical physics, the other in sociology), both have unique approaches to doing network science (see Borgatti et al. 2009 for a high-level comparison of these two branches of network science, with an emphasis on differences in what constitutes a theoretical contribution), and the relationship between the two fields has been difficult at times.

For example, many in social network analysis were frustrated by the group of physicists who became interested in the properties of ‘small world’ networks following the publication of a paper by Duncan Watts and Steven Strogatz (1998), which built on Stanley Milgram’s pioneering work on small worlds (1967; Travers and Milgram, 1969) and the literature on random networks that had grown up around this. Barabási (2002) and Watts (1999; 2003) suggested that these ideas could be applied to the social world, egregiously ignoring the work on social networks that had already been undertaken by sociologists, anthropologists, economists, and political scientists. Despite this lack of awareness of prior research, their ideas have begun to contextualise established work on network structures and their development over time.

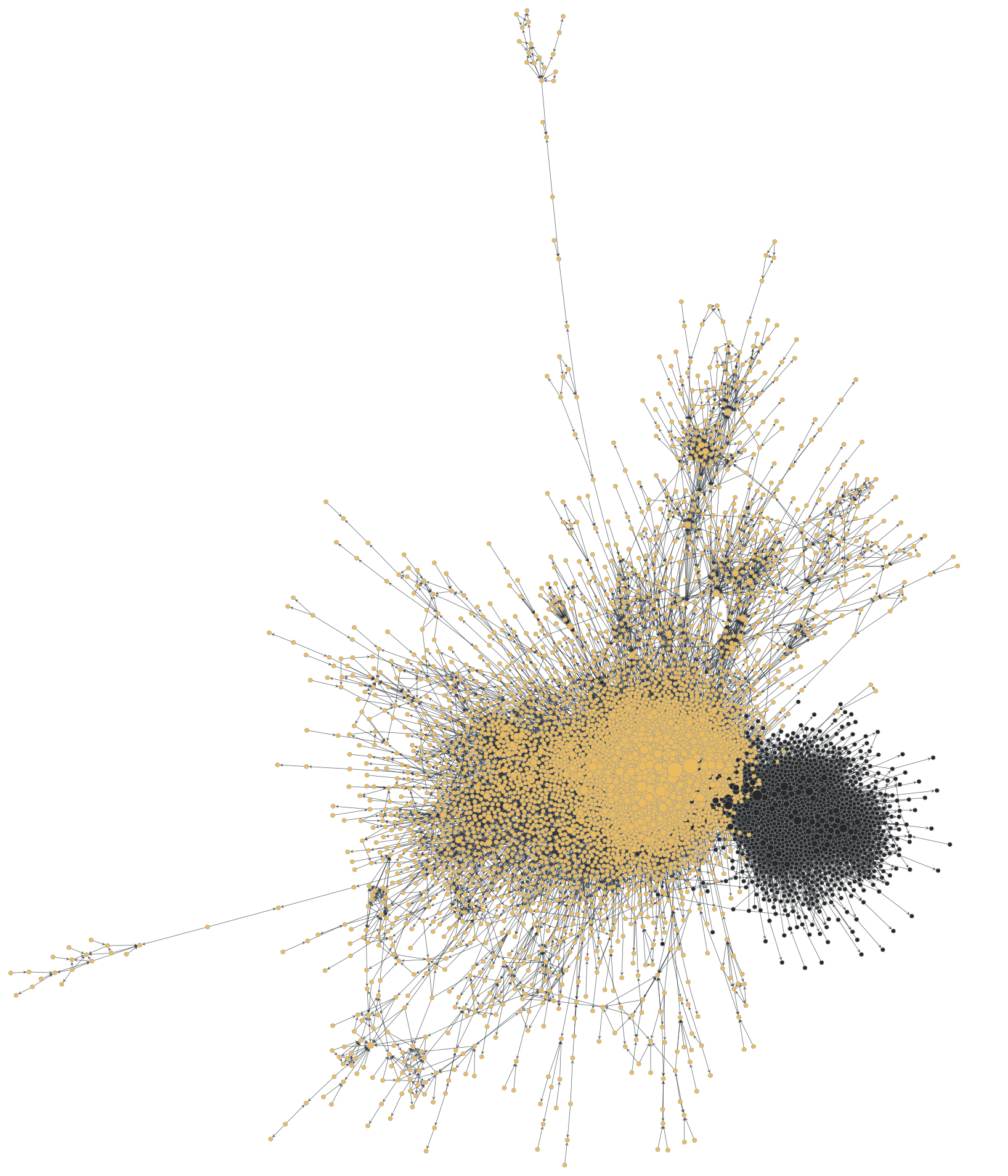
Freeman’s (2004) history of social network analysis undertook a network analysis of citation patterns in research on social networks and showed that the work published by Barabasi and Watts had rarely cited work by social scientists. It also disclosed, however, that social network analysts had been reluctant to engage with the work of the physicists. To some extent, the divide between social network analysis and network analysis in physics is still salient. Figure 3 is a visualization of a citation network consisting of all network analysis articles published in Social Networks and Physical Review E (filtered to articles containing the word ‘network’ in the title or abstract), with physics publications shown in gold and social networks publications shown in black. The separation between the two fields is clear, but we should expect this given well-known disciplinary differences (Borgatti 2009). Furthermore, the fact that these two approaches to network analysis are differentiated while still being densely connected is a promising sign for the evolving relationship between our fields.

Figure 3: Citation network of articles published in Social Networks and Physical Review E (filtered to articles that contain ‘network’ in the title or abstract). Physics publications are shown in gold, and Social Networks publications in black.

In general, it seems the division between network analysis in the social sciences and physics is breaking down and we are seeing productive intellectual engagements within and across disciplinary bounds. Citations aside, Watts moved into sociology long ago, and sociologists have debated and built on his contributions (Freeman, 2011; Scott, 2011). More recently, the INSNA Sunbelt conference was held jointly with NetSci at Indiana University in 2021, and the interdisciplinary journal Network Science was founded in 2013 with editors from both social and natural science disciplines (Brandes et al. 2013). Social network analysis can now be considered a sub-field – albeit a very large one – of a more general ‘network science’ (Newman et al., 2006; Newman, 2018 [2010]).

One area where the interdisciplinarity of network science has been especially productive is in modelling network dynamics (and, relatedly, dynamics on networks). Several major innovations have come from social network analysis (Stadtfeld et al., 2020; Snijders and Steglich, this volume; Schecter and Contractor, this volume; Centola, this volume), with some leading figures calling for the need to rethink foundational network concepts given the availability of timestamped streams of interactional data and extremely powerful computers (Kitts et al., this volume). Increased computing power has also greatly facilitated the development of generative approaches to network analysis, including stochastic actor-oriented models (Steglich and Snijders, 2022) and other approaches that utilize agent-based simulations one the one hand, and Bayesian probabilistic modelling (for nearly all contemporary network models) on the other.

Social network analysis is not a distinct theoretical approach. It is, however, a general theoretical orientation, or paradigm, and its methods have been employed in the development of many specific social theories. We can also think of it as a scientific community, or “invisible college” (Crane, 1972), with a recognizable intellectual lineage and clusters of researchers based in several centers and loosely linked by cross-cutting collaborations and inter-citations (Freeman, 2004). It is also a scientific institution, with dedicated journals (Social Networks, Journal of Social Structure, Connections, and Network Science), introductory textbooks (e.g. Degenne and Forsé, 1999 [1994]; Hanneman and Riddle, 2005; 2011a; 2011b; Knoke and Yang, 2008; Prell, 2012; Crossley et al. 2015; Robins, 2015; Scott, 2017 [1991]; Borgatti et al., 2022), handbooks for scholars and practitioners (Wasserman and Faust, 1994; Carrington et al. 2005; Scott and Carrington 2011; Light and Moody 2020; and this volume), dedicated and specialist computer software (Borgatti et al., 2022; Browne at al., this volume), an association (the International Network for Social Network Analysis), and a presence in other professional associations, such as the more recently formed NetSciSociety.

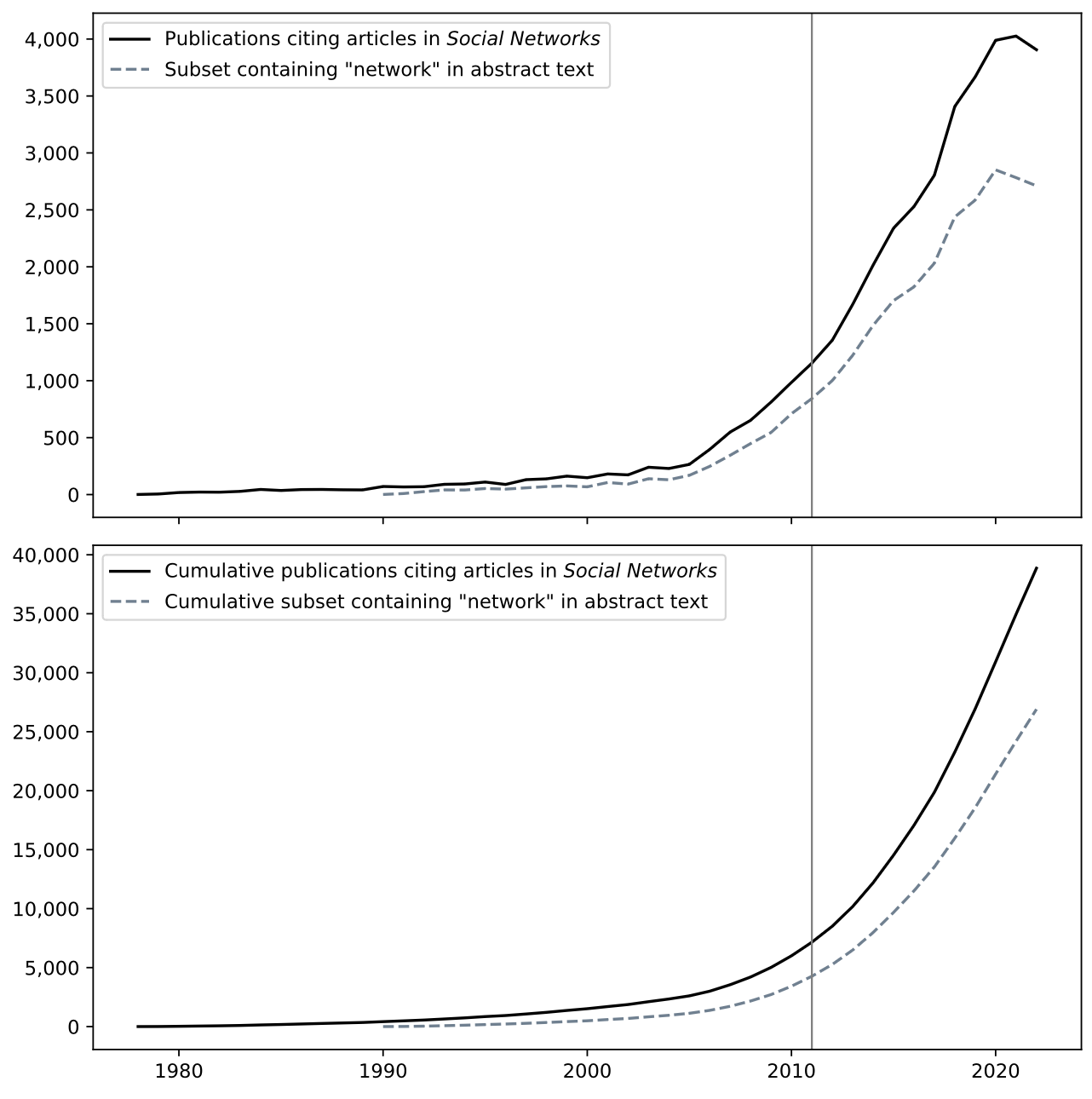
Since its take-off in the 1970’s, the volume of published research in social networks has grown exponentially. To approximate this growth, we collected metadata on nearly 40,000 articles indexed in the Web of Science (as of January 2022) that cite at least one article published in Social Networks. Within that collection, we label an article as an SNA publication if ‘network’ appears in the abstract.³ The results are shown in Figure 4, with the top subplot showing increases in the number of publications per year and the bottom subplot showing cumulative growth. The vertical line marks the publication of the first volume of this handbook in 2011, revealing how much the field has grown over 12 years. As of early 2023, we are approaching almost 2,500 new SNA articles published per year (likely higher), with over 25,000 publications in the field to date (likely higher). Neither the volume of published research nor the expansion of social network analysis into diverse subject areas (as previously discussed) show any signs of leveling off.

Figure 4: Growth of social network analysis over time. The top subplot shows the number of articles in the Web of Science that cite articles published in Social Networks, and the subset that also contain “network” in the abstract. The bottom subplot shows cumulative growth.

Central Ideas in Social Network Analysis

The mathematical ideas that underlie social network analysis are those of graph theory (Harary and Norman, 1953; Harary et al., 1965; Harary, 1969). This comprises a set of axioms and deductions about the relations between points and the lines connecting them that originated in Leonhard Euler’s (1736) mathematical investigations of the famous problem of the seven bridges of Königsberg. Euler investigated whether it was possible to walk through all city areas and islands while crossing each river bridge just once. He converted this practical problem into an abstract model of points and lines in which the points represented the areas of the city and the lines represented the bridges, and demonstrated mathematically that the task is impossible. Euler’s proof laid the foundations for studying networks of all kinds as graphs of points and lines.

Social network analysis, then, involves treating individuals and other social actors, such as groups and organizations as points or ‘nodes’, and their social relations as lines or ‘edges’. The various theorems of graph theory can then be used to describe and explore features of the social network. This mathematical model formalises the initial insight depicted in Moreno’s sociograms, and the theorems of graph theory provide a basis for analysing their formal properties. However, it is not necessary to draw a sociogram in order to use graph theoretical concepts and measures, as network data on any given social relationship can be recorded in matrices. A ‘sociomatrix,’ for example, would have rows and columns in the matrix to represent individuals or other social actors, with the presence, absence, or strength of a social relationship between each pair of individuals is recorded as a numerical entry in the cells of the matrix.⁴

Thus, the sociomatrix contains the same information as the corresponding sociogram: the rows or columns are its points and the contents of the cells are measures of the lines connecting them. While it can be very difficult, and often impossible, to calculate the properties of a large sociogram by visual inspection, matrices can be analysed using mathematical techniques (and therefore computers) regardless of the size of the network. Matrix models of graphs, then, allow a wide range of real social networks to be analysed and compared.

Graph theory is concerned with the structural properties of the configuration of points and lines that comprises the graph. Several extensions of the concept of the graph have been useful in social network analysis. For example, the ‘directed graph’ or ‘digraph’ takes account of the ‘direction’ of a line, to represent asymmetric relations such as friendship choices made or the flow of influence or resources between one actor and another. The ‘weighted’ or ‘valued’ graph can take account of the intensity or strength of a relationship by assigning a numerical ‘weight’ or ‘value’ to a line. In the ‘signed’ graph, the lines have positive or negative signs, which can represent sentiments or attitudes, among other things (Agneessens, this volume). In the ‘multigraph’, points may also be connected by multiple lines, each labelled by direction and value to represent a different type of relationship. Points may also have discrete- or continuous-valued properties, representing the attributes of the actors represented by the points, as in conventional social analysis. In mathematics, the term ‘network’ is used to describe these extensions to the basic idea of a graph, in which the lines and/or points have properties such as direction, valence, weight, multiplicity, etc. Thus, social network analysis is the analysis of systems of social relationships – social structures - represented by mathematical networks.

Special techniques must generally be used to obtain or generate network data (adams and Lubbers, this volume). Network data can be difficult to obtain and can raise unique problems of measurement validity and reliability, as well as particular ethical issues (both themes which are represented in our topic models of social networks research). Getting accurate and complete data on connections among the members of even a moderately large population (e.g. more than a dozen or so) by interviews or questionnaires can be impractical or subject to major inaccuracies – as the number of potential connections increases with the square of the number of members. At least three possible solutions to this problem are commonly used. First, data on connections may be collected from all members of the population, accepting the likelihood of inaccuracies, especially the inability of respondents to report all their existing connections. Second, data may be collected from a (possibly random) sample of members, who may also identify members who are omitted from the sample, and (possibly) also on their connections. Both approaches are likely to result in missing data on connections, which should be, but often are not, dealt with by special techniques for inference to the population (Krause and Huisman, this volume). The second approach results in a set of ‘ego-networks’ or ‘egocentric networks’, each centred on the ‘ego’ who was sampled (Crossley et al., 2015; Perry et al., this volume). A third approach is to use already existing data on connections among the entire population, typically from archived organizational records. This method entirely avoids problems of inference from samples, and may also avoid inadvertent ‘missing data’, as long as the data that were originally collected are accurate.

While the emphasis in social network analysis has been on quantitative data and analyses, qualitative and mixed-methods approaches are also used, and indeed these characterised much of the foundational anthropological work in social network analysis, as well as a growing body of recent work (Domínguez and Hollstein, 2005; Hollstein, this volume).

Once a social structure can be represented mathematically, a network analyst can measure such simple features as the overall ‘density’ of the network and the relative ‘centrality’ (Everett and Borgatti, this volume) of its points. A sociological analysis gives these concepts a substantive interpretation. For example, centrality measures have typically been used as indicators of power, influence, popularity, or prestige. Other network analyses based on graph theory include the investigation of cliques and clusters of points, structural divisions within a social network being seen in terms of the existence of particularly dense or well-connected subgroupings; or, equivalently, in terms of particularly sparse or poorly-connected areas of the network, representing points of potential cleavage (Moody and Mucha, this volume). Notions of local clustering, cleavage, and centrality have allowed the investigation of intermediary or brokerage roles (Burt, 2005), as well as the development of methods for ‘network reduction’, in which large, complex networks are reduced to smaller, more manageable realisations (Batagelj et al., 2014; Batagelj et al. this volume; Browne, Crick, and McLevey, this volume).

Most social network research has involved ‘one-mode’ analysis, where the rows and columns of the data matrix represent the same set of points, or social actors. Increasingly, however, researchers have investigated ‘two-mode’ networks in which there are two distinct classes of points, and the lines exclusively connect points of one class with points of the other class (Jasny, this volume). These are also called ‘affiliation’ networks, because they have often been used to represent the affiliations of people with organizations, although many other applications are possible. Two-mode data are represented in a rectangular matrix, in which the rows represent one type of point and the columns represent the other type. For example, one class of points could be persons and the other type could be events in which they were involved, or organizations to which they belong. Each cell entry indicates whether the indexed person is related to the indexed event or organization, or the strength, etc., of the relationship. Two-mode networks can easily be converted to one-mode networks with some loss of information, but among the most recent advances in social network analysis are the direct analysis of such features as centrality in two-mode networks (without first converting them to one-mode networks), and the extension of the concept of two-mode to multi-mode networks (Knoke et al., 2021; Jasny, this volume). The network-based topic models reported in this introduction, for example, are based on the direct analysis of bipartite networks of journal articles and words rather than one-mode projections of word co-occurrences.

Another recent extension of the basic network is the multilevel network, in which networks are hierarchically embedded in other networks; for example, the employees of an organization form a workplace network, which in turn is embedded in the interorganizational network formed by relationships among several or many such organizations. Analysis of such structures combines insights and statistical models developed for social network analysis and for multilevel analysis of conventional multilevel attribute data (Lazega and Snijders, 2016; Lazega and Wang, this volume).

While graph theory and network theory are basic to social network analysis, other mathematical models have also been used to analyse specific aspects of network structure. The algebraic approach used by Harrison White and others looks not at the properties of individuals and groups but at the structural properties of the social positions (or ‘statuses’) occupied by individuals, and the performed roles that are associated with these positions (Lorrain and White, 1971; Boorman and White, 1976; Pattison, 2011). These so-called positional approaches, or ‘blockmodels,’ use methods of matrix clustering to build on Homans’ early work and show how networks can be decomposed into hierarchical positions of the kind documented by Nadel (1957). These approaches have led to various ways of measuring and analysing the ‘structural equivalence’ or ‘substitutability’ of individuals within social positions, and to algebraic modelling of systems of compound social roles, corresponding formally to the more familiar systems of compound kinship roles (mother’s brother, wife’s father, etc.) developed by ethnographers (Doreian et al., 2005; Doreian et al., this volume). Recent developments in this area include the development of probabilistic generative models based on the idea of “stochastic equivalence,” and are grounded in Bayesian inference and latent variable modelling (Browne, Crick, and McLevey, this volume; see Blei (2014) on iterative data analysis with latent variable models).

As we have noted, networks larger than twenty or so points are difficult to draw accurately and legibly as sociograms. Multidimensional scaling was one of the earliest methods used to eliminate the random jumble of criss-crossing lines and so to order and display points in a way that retains spatial patterns inherent in relational data. Newer algorithms have greatly improved graph drawing, and researchers such as Batagelj and his colleagues (De Nooy et al. 2005; see also http://vlado.fmf.uni-lj.si/) and Krempel (2005; 2011) have been exploring alternative bases for network visualisation, including moving images of network change. Because network drawings are so useful for gaining an intuitive grasp of their structure, methods and software for network visualisation (or ‘graph drawing’) have received much attention from computer scientists (e.g. http://graphdrawing.org/symposia.html).

Many procedures for data analysis and statistical inference that are common in the social sciences (such as regression analysis, ANOVA, and various tests of statistical significance within the Frequentist paradigm) cannot be applied in network analysis without modifications, as they rely on the assumption that observations are independent of one another. This violates the central idea of network analysis: interdependence. This is one reason why, as previously discussed, technical contributions to network methodology have been so prominent in the field. A body of statistical theory, methods and software has been steadily developing that enables valid description and inference from network data (van Duijn and Huisman, 2011; Robins, 2015: chapter 10). Ove Frank (2011) has pioneered the investigation of inference from sampled network data, and conventional statistical models have been adapted for use with network data. Building on work by Frank and Strauss (1986), network statisticians have developed novel statistical techniques by generalising Markov graphs to a larger family of models (Wasserman and Pattison, 1996; Pattison and Wasserman, 1999; Robins et al., 1999; Lusher et al., 2013). The so-called exponential random graph model (‘ERGM’) resembles a logistic regression in which each pair of nodes in the graph is an ‘observation’, and the ‘dependent variable’ is the presence or absence of a connection between them. Solving the estimating equations for the parameters of the model provides estimates of the impact of such structural features of the graph as transitivity, reciprocity, etc., as well as of the attributes of the points. Most applications of the ERGM have been to simple graphs (i.e. with binary-valued edges), but methods and software have recently been developed to apply ERGMs to networks with weighted (valued) edges (Krivitsky, 2012; Huang and Butts, 2021; Krivitsky et al., 2021). ERGMs have become pervasive in contemporary network analysis. So much so that some feel ERGMs are being uncritically adopted as a kind of GLM for networks (see the discussion in Koskinen, this volume).

Until the beginning of this century, most social network analyses used cross-sectional data and static models. With the growing availability of longitudinal network data (especially multi-wave panel data) and time-stamped interaction data, new statistical models and methods for the analysis of change in networks over time have been developed. Agent-based computational methods have been used to explore processes of change in networks, relating structural transformations to the unanticipated consequences of individual-level decision making (Monge and Contractor, 2003; Steglich and Snijders 2022). Knowledge of the rules under which agents make decisions and act can be used to predict broad patterns of change in network structure. Networks change because of the ways in which individual actions are constrained by the structural locations of actors and the wider structural properties of the network (Centola, this volume). Tom Snijders has developed a powerful approach to this problem in which networks develop through the continual iteration of actions, and in which small, incremental changes can accumulate to a tipping point at which non-linear transformation in network structure occur (Snijders and van Duijn, 1997; Snijders, 2001; 2005; Snijders and Steglich, this volume). There are other widely-used models, such as Relational Event Models (Butts, 2008; Schecter and Contractor, this volume), that are designed for time-stamped interaction data.

Conclusion

In preparing this volume, we took the view that social network analysis is an evolving ‘paradigm’, rather than a theory or a method: that is, a way of conceptualizing and analysing social life

… that guides the selection of the social behavior data that are studied, influences the way these data are organized for analysis, and specifies the kinds of questions addressed. (Leinhardt, 1977: xiii)

In the most general terms, social network analysis is a structural paradigm: it conceptualises social life in terms of structures of relationships among actors, prioritizing them over the attributes of individual actors (cf. Breiger and Wagner-Pacifici, this volume). Harrison White’s comment that ‘subinfeudation reminds one of industrial decentralization’ (1963b: 77) highlighted structural rather than categorical parallels, and illustrates the kinds of questions and insights that arise from their study:

The same conundrums that baffled them baffle us. Just as William the Conqueror insisted on submission directly to himself from the chief vassals of his loyal lords… so a wise President seeks loyalty of subcabinet officers directly to himself. (White, 1963b: 78)

A social science paradigm comprises a theory or theories, a methodology or set of commonly employed methods, and a body of empirical research. This volume is organized around that tripartite division. Readers who are experienced in social network analysis can use this volume as a reference book, referring to particular chapters for up-to-date summaries of knowledge and indications of future trends, in a given topic area. Readers who are new to social network analysis may wish to begin with the introductory chapter by Prell and Schaefer before reading chapters on particular topics, and can start working with network data for the first time by following along with the introductory guide to network analysis software offered in Browne et al. (this volume). Alternately, a newcomer to social network analysis who is interested in a particular topic, such as gender or social policy, or in applications of social network analysis in a particular discipline, such as history or criminology, may prefer to start with the corresponding substantive chapter, referring back to the introductory, conceptual and theoretical chapters as necessary. In terms of theory, methods and substantive empirical work, this is an exciting time in social network analysis. The second edition of the SAGE Handbook of Social Network Analysis aims to be a one-volume state-of-the-art presentation of classic and contemporary views and to lay the foundations for the further development of the area.

References

An, Weihua. (2011) ‘Models and Methods to Identify Peer Effects.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. Los Angeles, CA and London, UK: Sage.

Arquilla, John and David Ronfeldt (2001) Networks and Netwars: The Future of Terror, Crime, and Militancy. Washington DC: Rand.

Azarian, G. R. (2005). The General Sociology of Harrison C. White. Houndmills: Macmillan.

Barabási, Albértó-Laszlo. (2002) Linked: The New Science of Networks. Cambridge, Mass.: Perseus.

Barnes, John A. (1954) ‘Class and Committee in a Norwegian Island Parish’, Human Relations 7: 39-58.

Batagelj, Vladimir, Patrick Doreian, Anuska Ferligoj, and Natasa Kejzar. (2014) Understanding Large Temporal Networks and Spatial Networks: Exploration, Pattern Searching, Visualization and Network Evolution. Chichester, UK: John Wiley & Sons.

Bearden, James, Atwood, William, Freitag, Peter, Hendricks, Carol, Mintz, Beth, and Schwartz, Michael. (2002 [1975]) ‘The Nature and Extent of Bank Centrality in Corporate Networks’. In Scott, J. (ed.) Social Networks. Vol. 3. London: Sage, 2002. Originally presented at the Annual Meetings of the American Sociological Association, 1975.

Blei, David. (2014) “Build, compute, critique, repeat: Data analysis with latent variable models.” Annual Review of Statistics and Its Application. 1(1): 203-232

Boorman, Scott A. and White, Harrison C. (1976) ‘Social Structure From Multiple Networks II: Role structures’, American Journal of Sociology 81: 1384-1446.

Borgatti, Stephen, Ajay Mehra, Daniel Brass, and Giuseppe Labianca. (2009). “Network analysis in the social sciences.” Science, 323(5916): 892-895.

Borgatti, Stephen P. and Virginie Lopez-Kidwell. (2011) ‘Network Theory’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Borgatti, Stephen P., Martin G. Everett, Jeffrey C. Johnson, and Filip Agneessens (2022) Analyzing Social Networks Using R. London: Sage.

Bott, Elizabeth. (1955) ‘Urban Families: Conjugal Roles and Social Networks’, Human Relations 8: 345-384.

Bott, Elizabeth. (1956) ‘Urban Families: The Norms of Conjugal Roles’, Human Relations 9: 325-341.

Bott, Helen. (1928) ‘Observation of play activities in a nursery school’, Genetic Psychology Monographs 4: 44-8.

Bourdieu, Pierre and Jean-Claude Passeron (1977 [1970]). Reproduction in Economy and Society. London: Sage.

Brandes, Ulrik and Thomas Erlebach (eds.). (2005) Network Analysis: Methodological Foundations. Berlin: Springer.

Brandes, Ulrik, Garry Robins, Ann McCranie, and Stanley Wasserman. (2013) “What is network science?” Network science 1(1): 1-15.

Buchanan, Mark. (2002) Small World: Uncovering Nature’s Hidden Networks. London: Weidenfeld and Nicolson.

Burt, Ronald S. (1982) Towards A Structural Theory of Action. New York: Academic Press.

Burt, Ronald S. (2005) Brokerage and Closure: An Introduction to Social Capital. New York: Oxford University Press.

Butts, Carter (2008) “A relational event framework for social action.” Sociological Methodology 38(1): 155-200.

Carrington, Peter J., Scott, John and Wasserman, Stanley (eds.). (2005) Models and Methods in Social Network Analysis. Cambridge: Cambridge University Press.

Cartwright, D. and Zander, A. (eds.). (1953) Group Dynamics. London: Tavistock.

Chua, Vincent, Julia Madej, and Barry Wellman. (2011) ‘Personal Communities: The World According to Me’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Crane, Diana. (1972). Invisible Colleges: Diffusion of Knowledge in Scientific Communities. Chicago: University of Chicago Press.

Crossley, Nick (2010) Towards Relational Sociology. London, Routledge.

Crossley, Nick (2021) ‘A Dependent Structure of Interdependence: Structure and Agency in Relational Perspective’ British Journal of Sociology. 56, 1, 166-182.

Crossley, Nick, Siobhan McAndrew, and Paul Widdop (eds) (2019) Social Networks and Music Worlds. London: Routledge.

Crossley, Nick, Elisa Bellotti, Gemma Edwards, Martin G Everett, Johan Koskinen, and Mark Tranmer (2015) Social Network Analysis for Ego-Nets. London: Sage.

David, Thomas and Gerarda Westerhuis (eds) (2014) The Power of Corporate Networks. A Comparative and Historical Perspective. London: Routledge.

De Nooy, Wouter, Mrvar, Andrej and Batagelj, Vladimir. (2005) Exploratory Social Network Analysis with Pajek. Cambridge, UK: Cambridge University Press.

Degenne, Alain and Michel Forsé. (1999 [1994]) Introducing Social Networks. London: Sage. Originally published as Les réseaux sociaux. Une approche structurale en sociologie. Paris: Armand Colin, 1994.

Donati, Pierpaolo (2012) Relational Sociology. A New Paradigm for the Social Sciences. London: Routledge.

Diani, Mario (1995) Green Networks: Structural Analysis of the Italian Environmental Movement. Edinburgh: Edinburgh University Press.

Diani, Mario. (2011) ‘Social Movements and Collective Action’ . In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Domínguez, Silvia and Betina Hollstein (eds) (2014) Mixed Methods Social Networks Research: Design and Applications. New York: Cambridge University Press.

Doreian, Patrick, Vladimir Batagelj, and Anuška Ferligoj (2005). Generalized Blockmodelling. New York, Cambridge University Press.

Emirbayer, Mustafa. (1997) ‘Manifesto For A Relational Sociology’, American Journal of Sociology 103: 281-317.

Emirbayer, Mustafa and Goodwin, Jeff. (1994) ‘Network Analysis, Culture, and the Problem of Agency’, American Journal of Sociology 99: 1411-54.

Emirbayer, Mustafa and Mische, Ann. (1998) ‘What is agency?’ American Journal of Sociology 103: 962-1023.

Euler, Leonhard. (1736) ‘Solutio problematis ad geometriam situs pertinentis’ [‘The solution of a problem relating to the geometry of position’]. Commentarii academiae scientiarum imperialis Petropolitanae 8: 128-140.

Fennema, Meindert. (1982) International Networks of Banks and Industry. Hague: Martinus Nijhof.

Fischer, Claude S. (1977) Networks and Places: Social Relations in the Urban Setting. New York: Free Press.

Frank, Ove. (2011) ‘Survey Sampling in Networks’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Frank, Ove and Strauss, David. (1986) ‘Markov graphs’, Journal of the American Statistical Association, 81 (395): 832-842 .

Freeman, Linton C. (2004) The Development of Social Network Analysis: A Study in the Sociology of Science. Vancouver: Empirical Press.

Freeman, Linton C. (2011) ‘The Development of Social Network Analysis–with an Emphasis on Recent Events.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Freeman, Linton C., White, Douglas R. and Romney, A. K. (eds.). (1989) Research Methods in Social Network Analysis. New Brunswick: Transaction Books.

Goyal, Sanjeev. (2011) ‘Social Networks in Economics’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Granovetter, Mark. (1973) ‘The Strength of Weak Ties’, American Journal of Sociology 78, 6: 1360-1380.

Granovetter, Mark. (1974) Getting A Job. Cambridge, Mass.: Harvard University Press.

Gerlach, Martin, Tiago Peixoto, and Eduardo Altmann. (2018) “A network approach to topic models.” Science Advances 4(7).

Gronlund, Norman E. (1959) Sociometry in the Classroom. New York: Harper & Bros.

Hanneman, Robert A. and Mark Riddle. (2005) Introduction to social network methods. Riverside, CA: University of California, Riverside At http://faculty.ucr.edu/~hanneman/

Hanneman, Robert A., and Mark Riddle. (2011a) ‘Concepts and measures for basic network analysis.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Hanneman, Robert A., and Mark Riddle. (2011b) ‘Concepts and Measures for Basic Network Analysis’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Harary, Frank. (1969) Graph Theory. Reading, MA: Addison-Wesley.

Harary, Frank and Norman, Robert Z. (1953) Graph Theory as a Mathematical Model in Social Science. Ann Arbor: Institute for Social Research.

Harary, Frank, Norman, Robert Z. and Cartwright, Dorwin. (1965) Structural Models: An Introduction to the Theory of Directed Graphs. New York: Wiley.

Helmers, H. M., Mokken, R. J. R., C. Plijter, C. and Stokman, F. N. (1975) Graven naar Macht. Op Zoek naar de Kern van de Nederlandse Economic. Amsterdam: Van Gennep.

Hoff, Peter, Adrian Raftery, and Mark Handcock. (2002) “Latent space approaches to social network analysis.” Journal of the American Statistical Association 97(460): 1090-1098.

Holland, Paul, Kathryn Blackmond Laskey, and Samuel Leinhardt. (1983) “Stochastic blockmodels: First steps.” Social Networks 5(2): 109-137.

Homans, George. (1950) The Human Group. London: Routledge and Kegan Paul, 1951.

Huang, Peng and Carter T. Butts. (2021) ‘Parameter estimation procedures for exponential-family random graph models on count-valued networks: A comparative simulation study.’ arXiv: 2111.02372. Nov 3.

Jennings, Helen Hall. (1948) Sociometry in Group Relations. Washington, DC: American Council on Education.

Kick Edward L. and Byron L. Davis. (2001) ‘World-system structure and change: An analysis of global networks and economic growth across two time periods’. American Behavioral Scientist. 44: 1561-1578.

Kick, Edward L., Laura A. McKinney, Steve McDonald, and Andrew Jorgenson. (2011) ‘A multiple-network analysis of the world system of nations, 1995-1999.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Kirke, Deirdre M. (2006) Teenagers and Substance Use. London: Palgrave-Macmillan.

Knoke, David (1990). Political Networks. Cambridge: Cambridge University Press.

Knoke, David. (2011) ‘Policy networks’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Knoke, David and Song Yang. (2008) Network analysis. 2nd ed. Beverly Hills, CA: Sage.

Knoke, David, Mario Diani, James Hollway, and Dimitris Christopoulos (2021) Multimodal Political Analysis. New York: Cambridge University Press.

Knoke, David, Franz Urban Pappi, Jeff Broadbent, and Yutaka Tsujinaka (1996) Comparing Policy Networks. Labor Politic in the US, Germany, and Japan. New York: Cambridge University Press.

Krempel, Lothar. (2005) Visualisierung komplexer Strukturen. Frankfurt: Campus Verlag.

Krempel, Lothar. (2011) ‘Network visualization’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Krivitsky, Pavel N. (2012) ‘Exponential-family random graph models for valued networks.’ Electronic Journal of Statistics 6: 1100-1128.

Krivitsky, Pavel N., David R. Hunter, Martina Morris and Chad Klumb. (2021) ‘ergm 4.0: New features and improvements.’ arXiv preprint. arXiv:2106.04997.

Lazega, E., & Snijders, T. (2015). Multilevel Network Analysis for the Social Sciences: Theory, Methods and Applications. Oxford: Springer.

Lee, Nancy H. (1969) The Search for an Abortionist. Chicago: Chicago University Press.

Leinhardt, Samuel (ed.). (1977) Social Networks: A Developing Paradigm. New York: Academic Press.

Lévi-Strauss, Claude. (1969 [1949]) The Elementary Structures of Kinship, rev. ed., Rodney Needham (ed.). Boston: Beacon Press. Originally published as Les Structures élémentaires de la Parenté. Paris: Mouton, 1949.

Levine, Joel H. (1972) ‘The Sphere of Influence’, American Sociological Review 37: 14-27.

Lewin, Kurt. (1936) Principles of Topological Psychology. New York: Harper and Row.

Light, Ryan and James Moody (eds.). 2020 The Oxford Handbook of Social Networks. New York: Oxford University Press.

Lin, Nan. (2001) Social Capital: A Theory of Social Structure and Action. New York: Cambridge University Press.

Lin, Nan, Cook, Karen S. and Burt, Ronald S. (eds.). (2001) Social Capital: Theory and Research. New Brunswick, NJ: Transaction.

Lorrain, Francois P. and White, Harrison C. (1971) ‘Structural equivalence of individuals in social networks.’ Journal of Mathematical Sociology 1: 49-80.

Lundberg, George A. and Lawsing, Margaret. (1937) ‘The Sociography of Some Community Relations’, American Sociological Review 2: 318-35.

Lundberg, George and Steele, Mary. (1938) ‘Social attraction-patterns in a village’, Sociometry 1: 375-419.

Lusher, Dean, Johan Koskinen, and Garry Robins. (2013) Exponential random graph models for social networks: Theory, methods, and applications. Cambridge: Cambridge University Press.

Milgram, Stanley. (1967) ‘The Small World Problem’, Psychology Today 2: 60-7.

Mische, Ann. (2003) ‘Cross-Talk in Movements: Rethinking the Culture-Network Link’, in Diani, M. and McAdam, D. (eds.) Social Movements and Networks: Relational Approaches to Collective Action. Oxford: Oxford University Press.

Mische, Ann. (2007) Partisan Publics: Communication and Contention across Brazilian Youth Activist Networks. Princeton, NJ: Princeton University Press.

Mische, Ann. (2011). ‘Relational sociology, culture, and agency’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Mitchell, J. Clyde. (1969a) ‘The Concept and Use of Social Networks’, in J. Clyde Mitchell (ed.) Social Networks in Urban Situations. Manchester: Manchester University Press.

Mitchell, J. Clyde (ed.). (1969b) Social Networks in Urban Situations. Manchester: Manchester University Press.

Monge, Peter R. and Contractor, Noshir S. (2003) Theories of Communication Networks. Oxford: Oxford University Press.

Moreno, Jacob L. (1934) Who Shall Survive? New York: Beacon Press.

Morselli, Carlo (2009) Inside Criminal Networks. New York: Springer.

Mullins, Nicolas C. (1973) Theories and Theory Groups in American Sociology. New York: Harper and Row.

Nadel, Siegfried F. (1957) The Theory of Social Structure. Glencoe: Free Press.

Newman, Mark. (2018 [2010]). Networks: An Introduction. 2nd ed. Oxford, UK: Oxford University Press.

Newman, Mark, Albert-László Barabási, and Duncan J. Watts (eds.). (2006) The Structure and Dynamics of Networks. Princeton, NJ: Princeton University Press.

Pattison, Philippa E. (2011) ‘Relation algebras and social networks.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Pattison, Philippa and Wasserman, Stanley. (1999) ‘Logit models and logistic regressions for social networks: II. Multivariate relations’, British Journal of Mathematical and Statistical Psychology 52: 169-93.

Prell, Christina (2012). Social Network Analysis: History, Theory and Methodology. London, Sage.

Putnam, Robert D. (2000) Bowling Alone: The Collapse and Revival of American Community. New York: Simon and Schuster.

Radcliffe-Brown, Alfred R. (1940) ‘On social structure’, The Journal of the Royal Anthropological Institute of Great Britain and Ireland 70: 1-12.

Radcliffe-Brown, Alfred R. (1957) A Natural Science of Society. Chicago: University of Chicago Press.

Robins, Garry. (2015) Doing Social Network Research: Network-based Research Design for Social Scientists. London: Sage

Robins, Gary L., Pattison, Philippa and Wasserman, Stanley. (1999) ‘Logit models and logistic regressions for social networks: III. Valued relations’, Psychometrika 64: 371-94.

Roethlisberger, F. J. and Dickson, W. J. (1939) Management and the Worker. Cambridge, Mass.: Harvard University Press.

Scott, John. (1986) Capitalist Property and Financial Power. Brighton: Wheatsheaf Books.

Scott, John. (1997) Corporate Business and Capitalist Classes. Oxford: Oxford University Press.

Scott, John. (2017 [1991]) Social Network Analysis, Fourth Edition. London: Sage.

Scott, John. (2010) ‘Social Network Analysis: Developments, Advances, and Prospects’, Social Network Analysis and Mining 1, 1.

Scott, John. (2011) ‘Social Physics and Social Networks’. In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Scott, John and Peter J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Scott, John and Griff, Catherine. (1984) Directors of Industry. Cambridge: Polity Press.

Steglich, Christian, and Tom AB Snijders. (2022) “Stochastic network modeling as generative social science.” In Klarita Gërxhani, Nan Dirk de Graaf, and Werner Raub (eds.) Handbook of Sociological Science. Edward Elgar Publishing.

Simmel, Georg. (1950 [1917]) Grundfragen der Soziologie (Individuum und Gesellschaft). Berlin and Leipzig: Walter de Gruyter, Trans. and ed. Kurt Wolff (1950), The Sociology of Georg Simmel. New York: Free Press.

Snijders, Thomas A. B. (2001) ‘The Statistical Evaluation of Social Network Dynamics’, in Sobel, M.E. and Becker, M.P. (eds.) Sociological Methodology, 2001. Oxford: Basil Blackwell.

Snijders, Thomas A. B. (2005) ‘Models for Longitudinal Network Data’. In Carrington, P. J., John Scott, and Stanley Wasserman (eds.), Models and Methods in Social Network Analysis. Cambridge: Cambridge University Press.

Snijders, Thomas A. B. and van Duijn, Marijtje A. J. (1997) ‘Simulation for Statistical Inference in Dynamic Network Models’. In Conte, R., Hegelmann, R. and Terna, P. (eds.) Simulating Social Phenomena. Berlin: Springer.

Snijders, Tom AB, Gerhard G. Van de Bunt, and Christian EG Steglich. (2010) “Introduction to stochastic actor-based models for network dynamics.” Social networks 32(1): 44-60.

Stokman, Frans, Ziegler, Rolf and Scott, John (eds.). (1985) Networks of Corporate Power. Cambridge: Polity Press.

Stadtfeld, Christoph, Tom A. B. Snijders, Christian Steglich, and Marijtje van Duijn (2020). ‘Statistical Power in Longitudinal Network Studies’. Sociological Methods and Research., 49, 1103-1132.

Sweezy, Paul M. (1939 [1953]) ‘Interest Groups in the American Economy’, in National Resources Committee, The Structure of the American Economy, Part 1, Appendix 13. Reprinted in Paul M. Sweezy, The Present as History. New York: Monthly Review Press, 1953.

Van der Hulst, Renée C. (2011) ‘Terrorist networks: the threat of connectivity.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Van Duijn, Marijtje A.J., and Mark Huisman. (2011) ‘Statistical models for ties and actors.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

Travers, Jeffrey and Milgram, Stanley. (1969) ‘An Experimental Study of the Small World Problem’, Sociometry 32, 4: 425-43.

Warner, W. Lloyd and Lunt, P. S. (1941) The Social Life of a Modern Community. New Haven: Yale University Press.

Wasserman, Stanley and Galaskiewicz, Joseph (eds.). (1994) Advances in Social Network Analysis. Beverley Hills: Sage.

Wasserman, Stanley and Faust, Katherine. (1994) Social Network Analysis: Methods and Applications. New York: Cambridge University Press.

Wasserman, Stanley and Pattison, Philippa. (1996) ’Logit models and logistic regressions for social networks: I. An introduction to Markov random graphs and p*’, Psychometrika 60: 401-26.

Watts, Duncan J. (1999) Small Worlds: The Dynamics of Networks Between Order and Randomness. Princeton: Princeton University Press.

Watts, Duncan J. (2003) Six Degrees. The Science of a Connected Age. New York: W. W. Norton.

Watts, Duncan J. and Strogatz, Steven H. (1998) ‘Collective Dynamics of “Small-World” Networks’, Nature 393: 440-2.

Wellman, Barry. (1979) ‘The Community Question: The Intimate Networks of East Yorkers’, American Journal of Sociology 84: 1201-31.

Wellman, Barry and Hogan, Bernard. (2006) ‘Connected Lives: The Project’, in J. Purcell (ed.) Networked Neighbourhoods. London: Springer-Verlag, 2006.

White, Douglas R. (2011) ‘Kinship, Class, and Community.’ In Scott, J. and P.J. Carrington (eds.), The SAGE Handbook of Social Network Analysis. London: Sage.

White, Harrison C. (1963a) An Anatomy of Kinship. Englewood Cliffs: Prentice-Hall.

White, Harrison C. (1963b) ‘Uses of Mathematics in Sociology.’ In James C. Charlesworth (ed.), Mathematics and the Social Sciences. Philadelphia, PA: American Academy of Political and Social Science.

White, Harrison C. (2008 [1992]) Identity and Control. 2nd ed. Princeton, NJ: Princeton University Press. First edition published in 1992.

White, Harrison C., Boorman, Scott A. and Breiger, Ronald L. (1976) ‘Social Structure From Multiple Networks I: Blockmodels of roles and positions’, American Journal of Sociology 81: 730-781.

Footnotes

1. Overviews of the history of social network analysis can be found in Freeman (2004); Prell (2012), and Scott (2017: Chapter 2).

2. The others consist of function words, as well as collections of words that are so common due to (a) their prevalence in nearly all SNA topics, or (b) article writing conventions.

3. Of course, like all methods, this approach is imperfect. Our two-step approach is designed to avoid false positives due to the widespread use of “network” as a metaphor, to differentiate between social network analysis and actor network theory, and so on. While this method may miss some social network analyses, we think the probability of a publication using social network analysis citing at least one article in Social Networks is very high. Among these articles, we consider any that contain ‘network’ to be an SNA publication. The final step in our approach mirrors that of others (CITES).

4. Matrices are also used for other types of network data, such as bipartite, multi-level, and multi-plex networks.